Send me and E-mail
ALETHEIA
THE FIBONACCI SEQUENCE
Along with phi/the golden ratio, the formation of our universe is governed by the unique properties of a corresponding number series known as the Fibonacci Sequence, which was discovered by mathematician Leonardo Fibonacci around the year 1200. Phi and the Fibonacci sequence are inherently connected, and are simply different expressions of the same thing; Phi being a ratio, and Fibonacci being a sequence.
The Fibonacci Sequence is described as a series of numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
The next number is found by adding up the two numbers before it.
The 2 is found by adding the two numbers before it (1+1)
The 3 is found by adding the two numbers before it (1+2),
And the 5 is (2+3), and so on…
Example: the next number in the sequence previously mentioned is 21+34 = 55
Here is a longer list:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...
When we make squares with those widths, we get a nice spiral:

This sequence ties directly into the Golden ratio because if you take any two successive Fibonacci numbers, their ratio is very close to the Golden ratio. As the numbers get higher, the ratio becomes even closer to 1.618. For example, the ratio of 3 to 5 is 1.666. But the ratio of 13 to 21 is 1.625. Getting even higher, the ratio of 144 to 233 is 1.618. These numbers are all successive numbers in the Fibonacci sequence.
In fact, manifestations of the Fibonacci sequence or golden ratio/spiral, appear in all forms of nature and science.
Some examples include:
Flower petals: The number of petals on certain flowers follows the Fibonacci sequence, where each petal is placed to allow for the best possible exposure to sunlight and other growth factors.


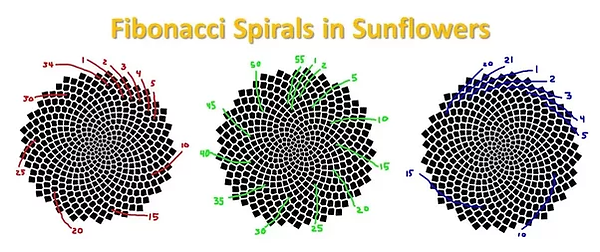
Seed heads: The seeds of a flower are often produced at the center and migrate outward to fill the space. For example, sunflowers follow this pattern.

Pinecones: The spiral pattern of the seed pods spiral upward in opposite directions. The number of steps the spirals take tend to match Fibonacci numbers.


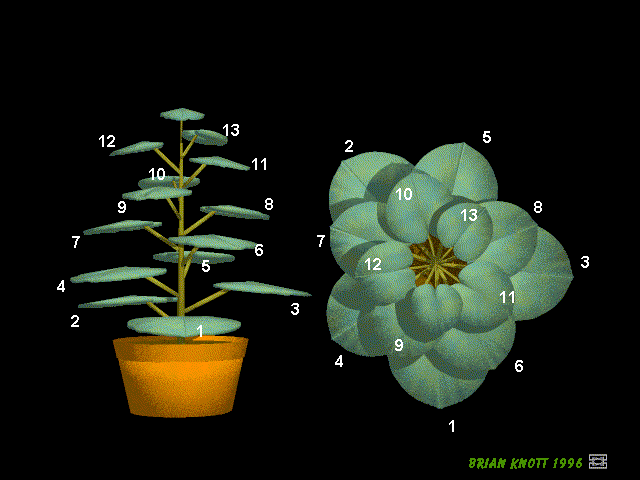
Tree branches: The way tree branches form or split is an example of the Fibonacci sequence. Root systems and algae exhibit this formation pattern.

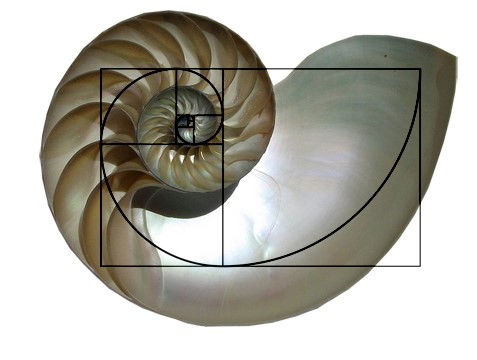
Shells: Many shells, including snail shells and nautilus shells, are perfect examples of the Golden spiral.
Spiral galaxies: The Milky Way has a number of spiral arms, each of which has a logarithmic spiral of roughly 12 degrees. The shape of the spiral is identical to the Golden spiral, and the Golden rectangle can be drawn over any spiral galaxy.

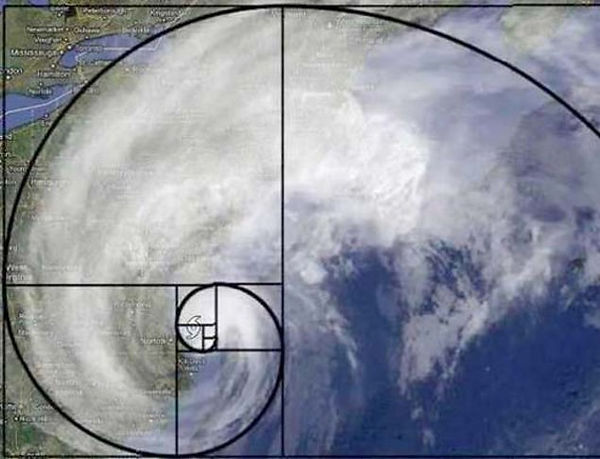
Hurricanes: Much like shells, hurricanes often display the Golden spiral.