Send me and E-mail
ALETHEIA
PHI/THE GOLDEN RATIO
Everything in this universe is constructed by a ratio known as Phi, which is commonly referred to as The Golden ratio: a special number found by dividing a line into two parts so that the longer part divided by the smaller part is also equal to the whole length divided by the longer part. It is often symbolized using phi (Φ), after the 21st letter of the Greek alphabet. Although this ratio has been present and occurring since the beginning of the universe, the term "phi" was originally coined by American mathematician Mark Barr in the 1900s. As with pi (π) otherwise known as the ratio of the circumference of a circle to its diameter, the digits of phi go on and on, theoretically into infinity.
In an equation form, phi (Φ) looks like this: a/b = (a+b)/a = 1.6180339887498948420…
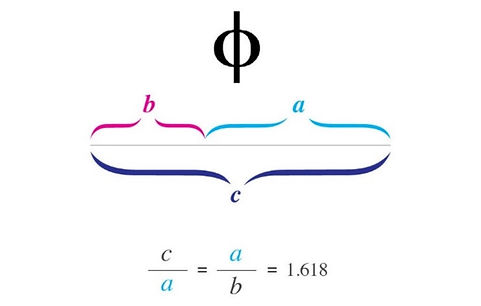
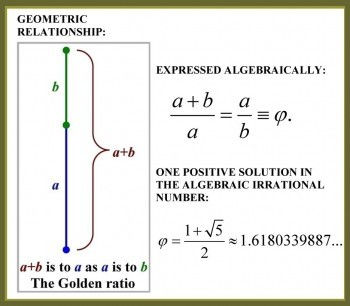
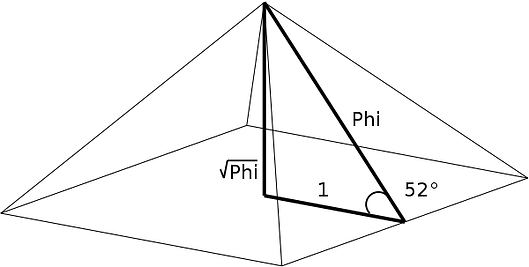
Phi is usually rounded off to 1.618. This number has been discovered and rediscovered many times, which is why it has so many names — the Golden mean, the Golden section, divine proportion, etc. Historically, the number can be seen in the architecture of many ancient creations, like the Great Pyramids. In the Great Pyramid of Giza, the length of each side of the base is 756 feet with a height of 481 feet. The ratio of the base to the height is roughly 1.5717, which is close to the Golden ratio.

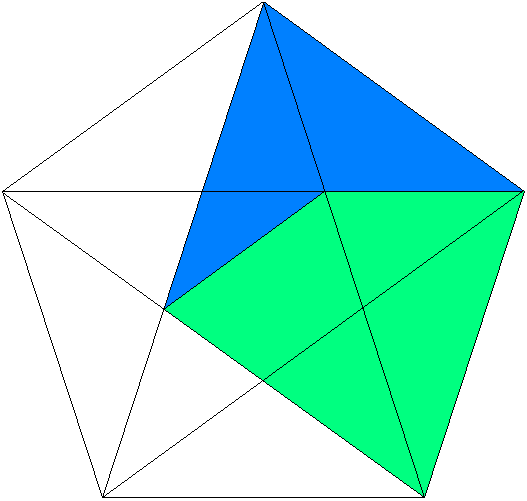
Phidias (500 B.C. - 432 B.C.) was a Greek sculptor and mathematician who is thought to have applied phi to the design of sculptures for the Parthenon. In addition, Plato (428 B.C. - 347 B.C.) considered the Golden ratio to be the most universally binding of mathematical relationships. Furthermore, Euclid (365 B.C. - 300 B.C.) linked the Golden ratio to the construction of a pentagram.
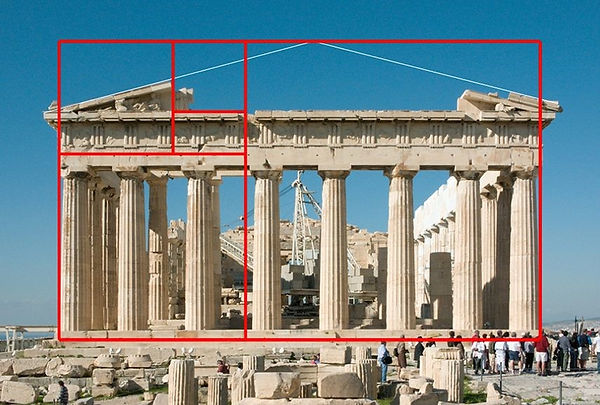
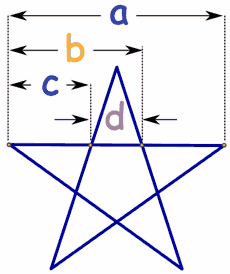
These phi ratio can be applied to the proportions of a particularly special rectangle, called the Golden rectangle. This is known as one of the most visually satisfying of all geometric forms – hence, the appearance of the Golden ratio in architecture and art.

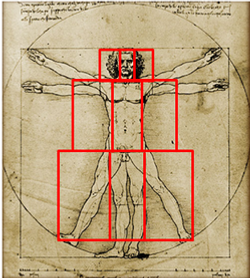
In 1509, Luca Pacioli wrote a book that refers to the number as the "Divine Proportion," which was illustrated by Leonardo da Vinci. Da Vinci later called this sectio aurea or the Golden section. The Golden ratio was used to achieve balance and beauty in many Renaissance paintings and sculptures. Da Vinci himself used the Golden ratio to define all the proportions in his Last Supper, including the dimensions of the table, and the proportions of the walls and backgrounds. The Golden ratio also appears in Da Vinci's Vitruvian Man and the Mona Lisa. Other artists who employed the Golden ratio include Michelangelo, Raphael, Rembrandt, Seurat, and Salvador Dali.


Other examples of the phi ratio which are found in architecture such as The Taj Mahal, The Eiffel tower, and Notre Dame.



Throughout history, phi has continued to appear in mathematics and physics, including the 1970s Penrose Tiles, which allowed surfaces to be tiled in five-fold symmetry. Another notable discovery occured in the 1980s, when phi appeared in quasiperiodic crystals, which was considered a newly discovered form of matter at the time. The quasiperiodic crystal was considered an "impossible" atomic arrangement, which was discovered by Dan Shechtman in 1982. Basically, a quasicrystal is a crystalline structure that breaks the periodicity (meaning it has translational symmetry, or the ability to shift the crystal one unit cell without changing the pattern) of a normal crystal for an ordered, yet aperiodic arrangement. This means that quasicrystalline patterns will fill all available space, but in such a way that the pattern of its atomic arrangement never repeats.


While most of the current applications of quasicrystals are rather mundane, such as the coating for frying pans or surgical utensils, Glotzer and Engel's simulation of a self-assembling icosahedral quasicrystal opens up exciting new avenues for research and development, such as improved camouflage capable of redirecting light to change the appearance of something.
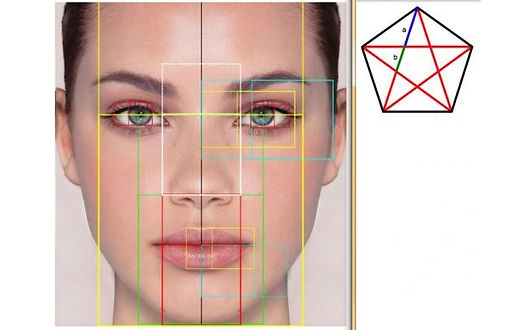
Phi is more than just a hidden design underlying the formation of the universe, or an obscure term found in mathematics or physics; it appears around us in our daily lives, even in our aesthetic views. Studies have shown that when test subjects view random faces, the ones they deem most attractive are those with solid parallels to the Golden ratio. Faces judged as the most attractive show Golden ratio proportions between the width of the face and the width of the eyes, nose, and eyebrows. The test subjects weren't mathematicians or physicists familiar with phi — they were just average people, and the Golden ratio appeared to elicit an instinctual reaction within the test subjects.

Further examples of the phi ratio can be seen throughout our physical bodies. The length of our fingers, each section from the tip of the base to the wrist is larger than the preceding one by roughly the ratio of phi. The measurement of the human navel to the floor and the top of the head to the navel is the Golden ratio. But we are not the only examples of the Golden ratio in the animal kingdom; dolphins, starfish, sand dollars, sea urchins, ants and honeybees also exhibit the proportion.
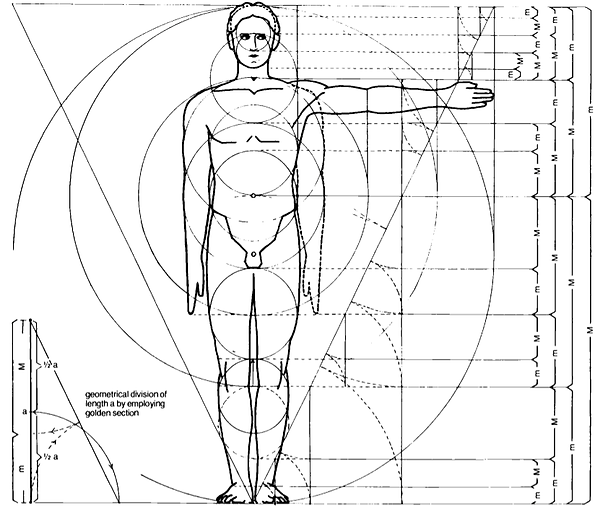
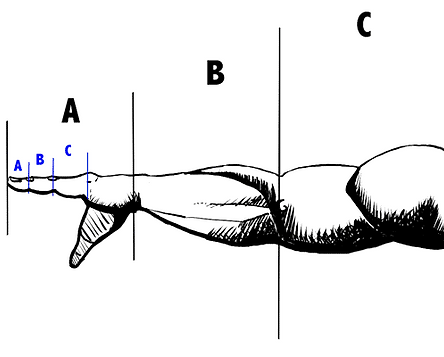
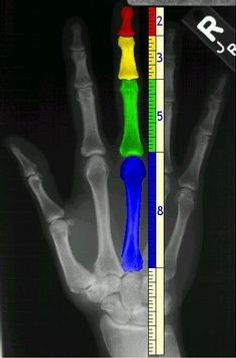
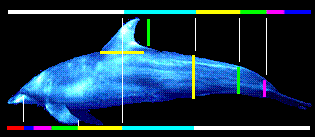
Also, a DNA molecule measures 34 angstroms by 21 angstroms at each full cycle of the double helix spiral, which fit into the ratio of phi. 34/21 = 1.61904762….
