Send me and E-mail
ALETHEIA
FRACTALS
In addition to the golden ratio and the Fibonacci sequence, the universe is organized by another mathematical phenomenon known as Fractals: a curve or geometric figure, each part of which has the same statistical character as the whole. Fractals are useful in modeling structures (such as eroded coastlines or snowflakes) in which similar patterns recur at progressively smaller scales, and in describing partly random or chaotic phenomena such as crystal growth, fluid turbulence, and galaxy formation.
A fractal is a natural phenomenon or a mathematical set that exhibits a repeating pattern that displays at every scale. If the replication is exactly the same at every scale, it is called a self-similar pattern. Fractals can also be nearly the same at different levels. Fractals also includes the idea of a detailed pattern that repeats itself. A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop.
Driven by recursion, fractals are images of dynamic systems – the pictures of Chaos. Geometrically, they exist in between our familiar dimensions. Fractal patterns are extremely familiar, since nature is full of fractals. For instance: trees, rivers, coastlines, mountains, clouds, seashells, hurricanes, etc.
What makes the Mandelbrot set so interesting is that this infinitely complex patterning is derived from a very simple formula. The basic formula for the Mandelbrot set can be generated by a computer calculating this simple equation over and over: Z = Z2 + C
The Mandelbrot set is determined by iterating with this equation. By iterating, I mean that we start with a value for Z and C. We plug these into the equation to get a new value for Z. We then plug that value for Z in and get a new Z, and so on…
VIDEO: The Mandelbrot Set (YouTube)
Two of the most important properties of fractals are self-similarity and non-integer dimension. What does self-similarity mean? If you look carefully at a fern leaf, you will notice that every little leaf - part of the bigger one - has the same shape as the whole fern leaf. You can say that the fern leaf is self-similar. The same is with fractals: you can magnify them many times and after every step you will see the same shape, which is characteristic of that particular fractal.

The non-integer dimension is more difficult to explain. Classical geometry deals with objects of integer dimensions: zero dimensional points, one dimensional lines and curves, two-dimensional plane figures such as squares and circles, and three-dimensional solids such as cubes and spheres. However, many natural phenomena are better described using a dimension between two whole numbers. So, while a straight line has a dimension of one, a fractal curve will have a dimension between one and two, depending on how much space it takes up as it twists and curves. The more the flat fractal fills a plane, the closer it approaches two dimensions. Likewise, a "hilly fractal scene" will reach a dimension somewhere between two and three. So, a fractal landscape made up of a large hill covered with tiny mounds would be close to the second dimension, while a rough surface composed of many medium-sized hills would be close to the third dimension.

Some examples of fractals include:
Tree branches and Romanesco broccoli:


Snowflakes and lightning:


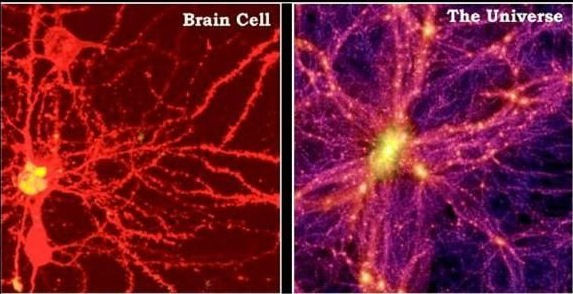
A brain cell and a computer-generated model of the universe: