Send me and E-mail
ALETHEIA
DIMENSIONS
Modern theories tell us that there are 10 spatial (or space-like) dimensions to our reality. The best explanation I have been able to find regarding the conceptualization of these dimensions was formulated by Rob Bryanston, who developed a creative way to use a variation of what's known as the point line plane postulate to visualize the 10 dimensions; a concept that most would have thought impossible for the human mind to ever comprehend.
First, we start with a point. Like the point we know from geometry, it has no size, no dimension. It's just an imaginary idea that indicates a position in a system.
a point ➤

A second point then can be used to indicate a different position, but it too is of indeterminate size. To create the first dimension, all we need is a line passing through any two points. A first-dimensional object has length only. No width, or depth.

two points ➤
first dimension ➤
A second point then can be used to indicate a different position, but it too is of indeterminate size. To create the first dimension, all we need is a line passing through any two points. A first-dimensional object has length only. No width, or depth.
If we now take our first dimensional line and draw a second line crossing the first, we've entered the second dimension. The object we're representing now exists within a plane that has length and width, but no depth.
2nd dimension ➤
Way back in 1884, a fellow named Edwin Abbott wrote a book about a race of two-dimensional creatures, called Flatlanders. Whether these imaginary creatures could really exist or not, they're useful for thinking about what it would be like to live in a flat, two-dimensional world.

For instance, if we were to watch a balloon passing through the Flatlanders world, it would start as a tiny dot, become a hollow circle which inexplicably grows to a certain size, and then shrinks back to a dot before popping out of existence.
balloon enters
2d plane ➤

balloon halfway through 2d plane ➤

But what would the flatlander actually see? The pictures below depict what it would look like to imagine the extremely limited viewpoint of a creature confined within this 2d plane.
balloon enters
2d plane ➤

balloon halfway through 2d plane ➤

Now, let's move on to the third dimension. This should be the easiest dimension to understand, because we exist within it during every moment of our lives. A three-dimensional object has length, width and depth.
3rd dimension ➤
But here's another way to describe the third dimension: if we imagine an ant walking across a newspaper which is lying on a table, we can pretend that the ant is a flatlander, walking along on a flat two-dimensional newspaper world.
ant→

--------- ➤

If that paper is now folded in the middle, we create a way for our flatlander ant to magically disappear from one position in his two-dimensional world, and be instantly transported to another.

ant →
step 1. ➤
step 2. ➤

ant →
step 3. ➤

← ant
We can imagine that we did this by taking a two-dimensional object and folding it through the dimension above, which is our third dimension. As we begin to imagine the extra dimensions, this will be an important concept to understand if we can think of the third dimension in this way.
2nd dimension ➤
folding through
3rd dimension ➤
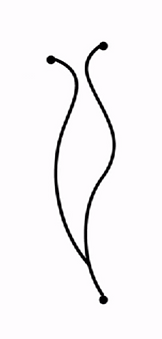
The third dimension is what you would fold through to jump from one point to another in the dimension below, the second dimension. To be clear, no matter what dimension you are folding, it provides a way to move instantaneously from one distant position to another. The scientific term for this concept is called a Wormhole: a hypothetical structure of space-time envisioned as a tunnel connecting points that are separated in space and time.

Now, let's look at the fourth dimension. Just like any other spatial dimension, it's made up of two opposing directions; but we 3d creatures only experience this dimension in one of those directions. Why is that?

It's because you and I are made out of 3d atoms and molecules, and we derive our energy from chemical reactions which move in one direction only. But science shows us the times reverse direction is just as valid; and in fact, the standard definition of antimatter is that it's matter which is moving backwards in time.

So, rather than saying the fourth dimension is time, let's use the word duration. If you were to imagine your body's duration as a shape in the fourth dimension, you could think of it as a long undulating snake, with your embryonic self at one end, and your deceased self at the other.

But because our reality is observed as one quantum frame after another from the third dimension, we are comparable to the second dimensional flat-landers. Like the flatlander who could only see cross-sections of objects from the dimension above, we as three-dimensional creatures can only see cross-sections of our fourth dimensional self. And just as you and I require the fourth dimension to change from state to state, like a 2d flatlander, time would be one of the two possible directions in the third spatial dimension.


1. ➤
2. ➤
3. ➤

4. ➤

Quantum mechanics tells us that the particles that make up our world are derived from waves of probability, simply by the act of observation. It is for this reason that I like to refer to the fifth dimension as our probability space.
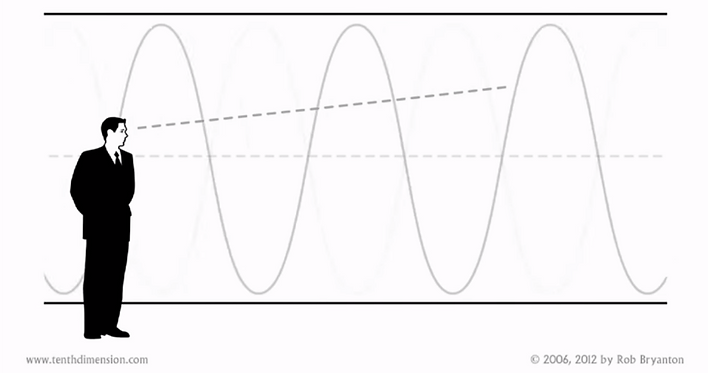
This relates very nicely to a theory which is now gaining acceptance. Advanced in 1957 by Hugh Everett the III, his theory is commonly known as the many-worlds interpretation of quantum mechanics. It was Everett who showed us that these parallel outcomes reside within a space which is orthogonal to space-time, and the versions of the universe that we don't observe, are just as real as the ones we do. This leads us to the conclusion that Everett's many-worlds reside within the fifth dimension.

What's orthogonal or at right angles to space-time? One of the most intriguing aspects of this approach to visualizing each new dimension as being orthogonal to the previous one, is that it means we can be observing one dimension, and be unaware of our motion in an additional one.
1-D ➤

2-D ➤

3-D ➤

4-D ➤

5-D ➤

Here's a simple example: if we make a mobius strip by taking a long strip of paper, adding one twist to it, taping the ends together, and drawing a line down the length of it, then our line will eventually be on both sides of the paper before it meets back with itself.
1. ➤

2. ➤

3. ➤

4. ➤

5. ➤

It appears somewhat amazingly that the strip has only one side, so it must be a representation of a two-dimensional object. This means that a two-dimensional flatlander, traveling down the line we just drew, would end up back where they started, without ever feeling like they had left the second dimension. In reality, they would be looping and twisting in the third dimension, even though to them it felt like they were traveling in a straight line

The fourth dimension feels like a straight line to us, moving from the past to the future, with what some have called the arrow of time. But that arrow is, without us even being aware of it, actually twisting and turning in the dimension above. So, the long undulating snake that is us at any particular moment, will feel like it is moving in a straight line in the fourth dimension; but there will actually be a multitude of paths in the fifth dimension that we can branch to at any given moment. Those branches will be influenced by our own choice, chance, and the actions of others.
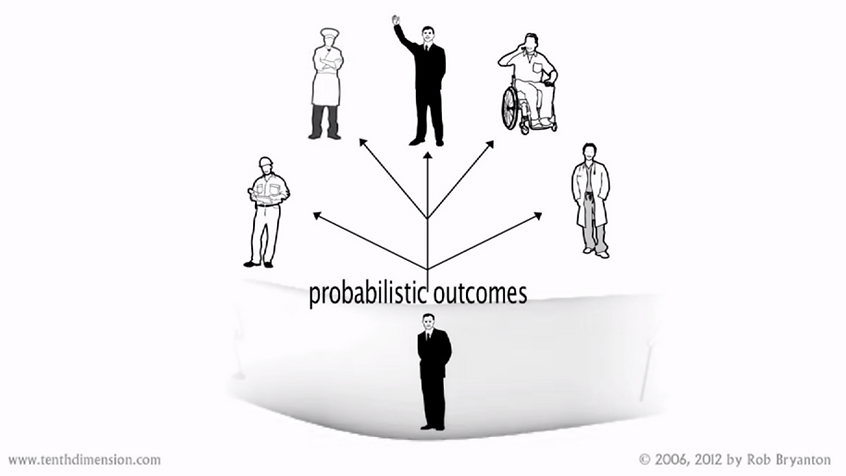
We move through those branches one clock frame at a time, and this is why some physicists say that the fifth dimension is curled up at the Planck length; because from our reference frame, that's how it appears. It's important to note though that Everett was also very clear that causality could not be violated as we observe one outcome or another. Right now, there is zero probability that you or I can suddenly be in the world where for instance Michael Jackson is still alive, and yet the many-worlds interpretation says those versions of the universe really exist within the quantum wave function. So, how could we get there? We would need to “fold” our 5-D probability space through the sixth dimension, also referred to as the universes Phase Space: a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space. Therefore, those points representing the versions of our universe where Michael Jackson is still alive, are inaccessible to us from our current position within the fifth dimension, but they still exist within our sixth dimensional phase space.

Now as we enter the seventh dimension, we're about to imagine a line which treats our entire sixth dimensional phase space as if it were a single point. You could say that this point represents what Einstein was thinking about when he said, “the separation between past, present, and future, is only an illusion.” Some would call this point infinity for our universe; all possible outcomes, all wrapped up as one, single, timeless everything.

So, if we intend to draw a seventh dimension a line that passes through this point, we need to be able to imagine what a different point in the seventh dimension is going to be; because that's what our line needs to pass through. But how can there be anything more than infinity? The answer is: there can be other completely different infinities. Other different everything's, created through initial conditions which are different from our own Big Bang. Different initial conditions will create different universes, where the basic physical laws such as gravity, or the speed of light, are not the same as ours. And the resulting branching time-lines from that universe’s beginning, to all of its possible endings, will create a phase space of all possible states, different than the phase space associated with our own universe.

Say for example that a 7d line might represent all possible universes, with different values for gravity, with our universe someplace on that line. Lower gravity the ours would be in one direction, and higher gravity in the other. Would that line be a way to get to every possible universe? No.
In order to represent other universes with the same value for gravity as ours, but with other basic physical constants changed, we need to branch off to the possibilities contained within the eighth dimensional phase space of all possible physical realities. And this would be true no matter what variables we were adjusting within the seventh dimensional line. We would still need the additional degree of freedom afforded by the eighth dimension to get to every possible physical universe.

Now, how do we get to the ninth dimension? the same logical rules we've been using would apply. If we were to instantaneously jump from one eighth dimensional point to another, without passing through the intermediate points, it would be because we were able to fold through the ninth dimension.
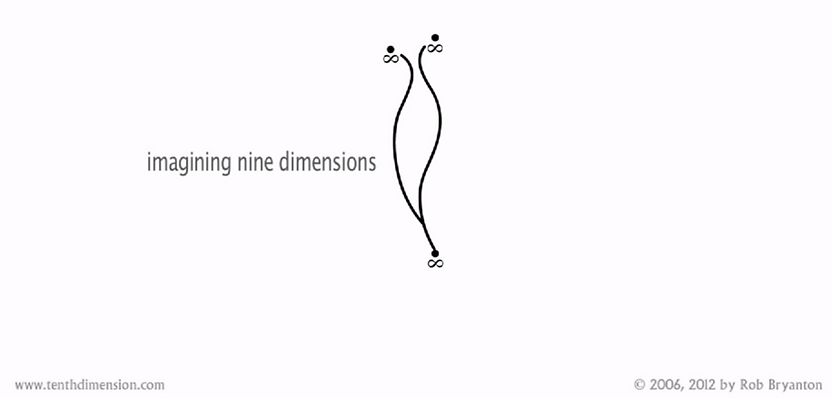
Within this approach to visualizing the dimensions, the ninth spatial dimension is beyond any physical reality, and is much more about information; a seething foam of possibilities which could represent impossible universes which exists only as concepts, or selection patterns which could be the beginning of a path toward a universe such as ours, or any other. And to complete the logic we have used from the outset, we now take the entire ninth dimension, and conceive of it as a single point. But this is where we hit a roadblock. If we're going to imagine the tenth dimension as continuing the cycle, and being a line, then we're going to have to imagine a different point that we can draw that line to. But it can't be done.
By the time we've imagined an ultimate ensemble of every conceivable information pattern, as a single point of indeterminate size, there's no place left to go. M-theory says that our reality is defined from ten spatial dimensions, plus time, and that's what we're talking about here; a tenth dimension without time. As soon as anything tries to happen within the tenth dimension, we are spilled back into the dimensions below, as subsets are carved out from this ultimate ensemble, this omniverse, this timeless and unchanging everything which underlies our reality, or any other. And that is a beautiful and fascinating idea for us all to ponder. – ‘Imagining the Tenth Dimension: A New Way of Thinking About Time and Space’. Rob Bryanton
Here is a video that explains the 10 dimensions: